This is my take on ARC 2025, a review of the literature, some opinions and attempts to categorize and conceptualize the various approaches so far, ideas that have been discussed, as well as what's special about the competition, what might work and what won't work.

If you are new to ARC and want an overview of the various approaches from 2024, I hope this is useful to you as well as me! The first half of the document covers high level approaches and key ideas extracted from various papers and results. The second half provides some more detail (although still fairly high level) on each of the papers that won in ARC 2024, as well as some hand-picked related papers, work and ideas.

Quite a lot of broad knowledge around ML/AI is assumed throughout. I have done my best to link to or explain some concepts, but this will probably be tricky if you don't know some basics around deep learning, and general ML terminology.

I have almost certainly made many mistakes, possibly at a conceptual level, and most definitely in some of my attempts to extract details and ideas out of the papers. There are a few "hot takes" in here too and I've not held back in expressing some opinions of my own - please take these with a pinch of salt, and I'm very open to feedback here.

I have not covered all the literature and read all the papers, there is a lot out there. If you think I've missed something important, please let me know.

An introduction to ARC #

ARC stands for the Abstraction and Reasoning Corpus, it is a benchmark that came out of François Chollet's paper On The Measure of Intelligence in 2019. It has evolved a few times, the benchmark renamed ARC-AGI, and recently an ARC-AGI-2 version was launched in March 2025.

Here is an example of an ARC puzzle. For each puzzle (or sometimes referred to as a task), you are provided with around 2-4 (usually 3) examples of input output grid pairs, and one (but occasionally 2) "test" input grid(s) for which you have to predict the output grid.

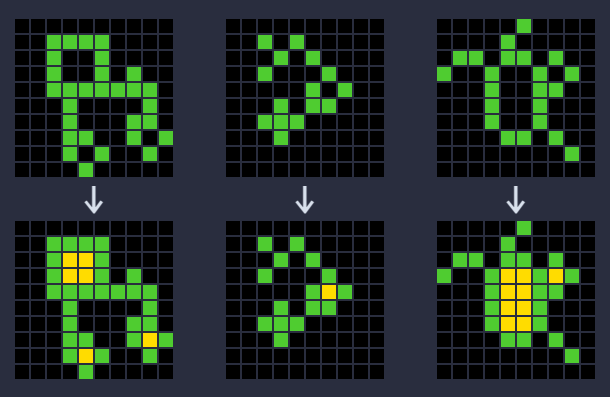
The goal is to infer the rule from the examples, and apply it to the test input grids. The puzzles always exist in this same grid world construct, but the space of possible puzzles is massive. The final ARC competition is run against a hidden test set of puzzles, which means a good solution must be able to do some amount of out of domain generalization.

At a high level ARC is designed to test "skill acquisition efficiency", and this would be the simplest way to capture what François defines intelligence as.

The intelligence of a system is a measure of its skill-acquisition efficiency over a scope of tasks, with respect to priors, experience, and generalization difficulty.

You can read a lot more about the details of the benchmark, the competition and explore the puzzles on the ARC website.

As I will reference these throughout, it's important to note that with both the 2024 and 2025 competitions, there are a few different datasets we care about:

training - fully public, 1000 tasks for v2, should contain puzzles that capture all the essential "core knowledge priors" and submissions are expected (but not required) to train on.
public eval - this is also a publicly available set of 120 tasks, expected to be used to evaluate and iterate on solutions locally, it could also be used as training data for private eval or test submissions.
semi-private eval - not publicly available, 120 tasks, this will be used for leaderboard standings throughout the competition. It is semi-private as some systems have been tested against it that are not sandboxed (e.g service provided LLMs) and there is a possibility of data leakage.
private eval (test) - this is fully hidden, solutions will only run against it once at the end of the competition for final scoring, leakage is highly unlikely.

What makes ARC special #

Out of domain generalization

When it comes to the private test set your solution program will be presented with new puzzles that it just hasn't seen before. This is a significant difference from many benchmarks, great ingenuity and creativity went into constructing these puzzles and while they may be composed of common elements, transformations, core knowledge priors that are present in the training set, they are ultimately different problems.

People seem to often be surprised by this and just how different the test problems are! Solutions that could easily overfit to the training set could end up scoring 0% on the hidden test set.

This is, I believe, the most important thing to understand about ARC. The challenge here is to generalize out of the domain of the training dataset in a way that most Deep Learning often fails to.

The outcome of this is that some form of test time adaptation is absolutely crucial for getting a good score on the benchmark, and we'll see this as a major theme in the results from 2024.

Compute efficiency

The second most important thing to understand about the challenge comes back to Francois' definition of intelligence - "The intelligence of a system is a measure of its skill-acquisition efficiency over a scope of tasks...".

Efficiency is an explicit part of the challenge. There are deliberate compute bounds for submissions, effectively in terms of FLOPs. You have a machine with a fixed specification and a capped running time. You must use this compute efficiently to succeed. Unrestricted scaling is not what the benchmark is for.

And as with the above, this is the point! It's easy to critique this and say, well if we got GPT4.5 or O3 and threw $1M of compute at it we could solve ARC (kind of like how O3-high basically did that for ARC-AGI-1 in December 2024). But, that is not very efficient [0] skill acquisition, and we already know in principle that we can get logarithmic returns on inference time compute.

Without efficiency as an explicit goal, ARC would simply not be an interesting benchmark.

A baseline learning architecture for ARC #

Given the context on ARC, it is hopefully clear why you can't "just" throw any pre-trained model using a standard deep learning architecture at it. People have tried, and it doesn't work well (with a carve out for thinking models, discussed below).

At the other end of the spectrum we have a whole category of approaches that come from the world of discrete program search (also referred to as program synthesis, and sometimes program induction). One of the nice things about coming at ARC from this angle is that we can lay out a (horribly inefficient) architecture of a learning system that should solve ARC with enough compute. This gives me an opportunity to define some useful terminology for the rest of the post so let's lay it out!

Let's start by making the very reasonable assumption that it is always possible to write some program that can capture the rule of any given ARC puzzle, and produce the output grid from the input grid, more formally:

There exists a Turing-complete language L, that can represent all possible programs P that map from some representation of a grid X to grid Y.

This must be true if we accept things like the principle of computational equivalence or the notion of Turing-completeness. An obvious (but perhaps not the best) candidate for such a language would be a modern turing-complete programming language such Python.

The second thing we need to do is be able to enumerate all possible programs P that are formed out of our language L. This is generally possible, even for Python there is nothing stopping us from just listing sequences of bytes as the program source, even if most such programs will immediately fail.

For each puzzle we then:

Find the shortest program within P that solves all the example grid pairs.

Given the above, we know that such a program must exist.

Despite the set of programs P being of infinite size, as we are looking for the shortest such program then provided we can enumerate our programs in at least roughly size order, that is not a problem.

Why the shortest? This comes from a few well known theoretical ideas, e.g the minimum-description length principle, Solomonoff induction, Occam's razor, Kolmogorov complexity, etc. I won't write about this in depth here, you can read about them, but in general we are now also accepting the idea that "the simplest explanation is the best explanation".

This relatively dumb approach will probably work provided a few details are right. The problem is it's horribly inefficient, and we don't have infinite compute. So a significant amount of research is about making this approach more efficient, and there are a whole bunch of ways you could do this:

Creating domain-specific languages (DSLs) for ARC that are more efficient to search and enumerate than a fully general purpose language such as Python, which you will see come up in nearly every paper below, even the LLM based ones
Implementing program enumeration and validation as compute efficiently as possible, perhaps even running on GPUs, or some nicely multi-threaded C code
Searching intelligently - within a language, we can get smart about which parts of the program space to search, and this can leverage deep learning, manual heuristics, or building up vocabularies of composable programs, there are many approaches here explored below.
Optimizing selection criteria - shortest program length might oversimplify a little or have slightly varying definitions, we can also see how our programs perform under multiple augmentations of the data, or even combine multiple discovered correct programs.

Nearly all the top papers and results go after some of the above opportunities, and this is broadly what Francois has been saying is the approach he thinks is most likely to deliver results on ARC - Deep learning guided program synthesis. This is also effectively what he and Mike Knoop started a company to explicitly work on:

(w.r.t NDEA) Our first focus is on deep learning-guided program synthesis to create AGI that can invent, adapt, and innovate

Key ideas and the technical report #

At the end of the 2024 competition the ARC team released a technical report covering top scores, top papers, companies and a summary of approaches. It's relatively brief, but I'll highlight a few things from it, or you can read it: ARC Prize 2024: Technical Report.

The 2024 ARC competition saw a shift away from the dominance of discrete program search approaches that had prevailed in previous years. This year, LLMs became a significant factor, driving both new program induction approaches and transductive approaches, with the crucial introduction of test-time fine tuning. Additionally, ensembling played a key role in improving scores for the top papers.

If we look back at the 2020 competition, the winning result that stood for quite a long time called Icecuber was a fairly dumb brute force discrete program search. LLMs out of the box performed poorly, but, with a slew of test time adaption methods being developed for them they quickly started to take over.

One of the standout claims for me from the report was:

One approach that has not been tried so far (likely because it is technically challenging) but that we expect to perform well in the future, is the use of specialist deep learning models to guide the branching decisions of a discrete program search process - similar to what can be seen in the AlphaProof system from Google DeepMind.

I.e no one has tried exactly what Francois thinks will work. There are certainly many papers that attempt to do something like this conceptually, but are not implemented literally as a specialist DL guided program search (for example, the DreamCoder based approaches).

Smart vs efficient search #

One more highlight from the report:

We also note that deep learning-guided program synthesis does not currently decisively beat DSL-based brute-force program search

You have a spectrum here - search smartly - search fast. No one has come up with a DL model that can effectively outperform a well engineered brute-force search, yet. Your NN and search policy network has to deliver more value than its relatively high computational cost.

There is a good analogy here to progress in Chess/Go. For example in chess, Stockfish has been the most consistently capable chess bot over the last 10 years but used no neural networks or learned search policy, just some heuristics and a very efficient and well engineered search algorithm.

It wasn't until 2020 when that trade-off started to make sense for Stockfish and they moved to some sort of NN based policy. We saw a similar concept behind Go. Heuristic based brute force search was no match for humans until AlphaGo, where the breakthrough was ultimately having deep learning guide the search much more intelligently (and a lot of innovations to actually achieve that).

It seems [1] that humans search smartly, and probably most people assume that this will eventually be the winning approach for ARC that can "break" the logarithmic returns of a brute-force search, but within discrete program search approaches we just haven't seen this flip that way, yet.

We expect that more efficient program search techniques leveraging deep learning should be able to pull away from brute-force search in the future.

Transduction and induction #

Transduction and Induction are two phrases you will see a lot in the literature and in the rest of this write up, let's discuss them a little.

I've struggled a little with this terminology, and the formal definitions of transductive and inductive learning don't seem to help much. The abstract of the 1st prize paper below captures well what they tend to mean in the context of ARC:

Induction - inferring latent functions
Transduction - directly predicting the test output for a given test input

Inductive approaches generally mean finding (learning, inferring, inducing) a function that can solve the puzzle. You try to find a good program, then you apply it to the test input (more along the lines of discrete program search). It offers an explanation for the observed data in the form of a program.

Transductive approaches skip that step, they just go for it, generate the output based on some prior knowledge (more along the lines of just giving an LLM the examples and hoping it does some in-context learning). They do not offer an explanation [2].

I don't think this is a well defined distinction and gets particularly blurry when looking at some of the TTT (test-time-training) fine tuning approaches, and also with thinking language models. It also depends on where you draw the line around a system.

For the TTT case, if you think of an LLM and its weights as a program [3] - and then at test time you fine-tune your weights to better reproduce the example problems - you are clearly doing some sort of program inference, it's just not on a discrete program. Something to this effect is noted in the technical report:

Interestingly, TTT can be seen as conceptually similar to program search, albeit at the opposite end of the memorization/recombination spectrum.

One difference here however, is that a fine-tuned model offers no easily interpretable explanation.

Ensembling #

One of the results called out in the technical report is the value of ensembling both transductive and inductive methods, which was the main point of one of the papers below. Ensembling across both methods was crucial to get to the top of the leaderboard in most cases [4].

Ensembles are a mainstay of ML, and frequently pop up in winning kaggle competitions. If you want a good score, this is a relatively cheap way to boost it. Notably, 2 of the leaderboard results in 2024 were ensembles of previous years submissions.

Some of the papers discussed below make some interesting observations about what ensemble well together (e.g a mix of transductive and inductive learners), but the mechanics of ensembling are relatively simple so there isn't a tremendous amount to dig into here.

Domain-specific-languages (DSLs) #

Improvements in DSLs was a significant driver of progress early on in the first few years of ARC being released. Michael Hodel authored ARC-DSL, one of the original DSLs for ARC, as an example that is still relevant and useful today.

A good DSL can greatly improve search efficiency, given it is what we search over. Pure Python is not a great language for brute-force search as most programs are completely irrelevant[5]. A good DSL for the domain can help ensure that solutions can be represented in a small program, and that most parts of the search space are actually valid programs that operate on grids.

One challenge with most of the DSLs is that they are hand-coded. The author of a DSL might go and solve all the ARC training tasks, and then produce a set of language primitives that are necessary to solve all the problems they have seen. Whilst this makes the search efficient, it's hard to guarantee they are complete. The ability to solve all the training tasks does not necessarily mean they have the ability to solve all of the test time tasks! This needs to be a primary objective of any DSL, be expressive enough whilst also providing a small yet useful set of primitives.

The DSLs often end up being rather large, for example, ARC-DSL contains a massive 160 primitive functions!

If you want to learn more about the construction of a DSL, then the ARC-DSL write-up is probably a good place to start. Probably avoid writing one yourself unless you are doing something very novel, although a number of the papers below do end up doing this.

Representations #

It is almost certainly the case that there is some transformation of the grid representation of ARC problems that makes them easier to solve than working on the grids directly themselves. Whether this is hard-coded, learned or otherwise, such a representation likely exists.

Parsing ARC grids into objects has been explored in some of the papers, e.g:

Graphs, Constraints, and Search
Object-centric Models and the MDL Principle

Representations for the ARC grids have been explored all the way back in 2022. The intuition here is probably that by mapping to some better data structure for representing the grids, the DSL becomes simpler, and the search process more efficient for programs that operate on those grids.

                                     
 ┌──────────┐           ┌──────────┐ 
 │  Input   │           │  Output  │ 
 │   Grid   │           │   Grid   │ 
 └────┬─────┘           └────▲─────┘ 
      │                      │       
      ▼                      │       
   Encoder                Decoder    
      │                      ▲       
      │                      │       
 ┌────▼─────┐           ┌────┴─────┐ 
 │ Abstract ├───────────► Abstract │ 
 │   Rep    │           │   Rep    │ 
 └──────────┘  Solve    └──────────┘ 
               this                  
               problem!

Representations can be related to the DSL itself but don't have to be. When treated as an explicit outer process, this approach is rather flexible, as these representations can then be fed into many different systems including LLMs, where for example one person claimed a doubling of O1 performance by mapping ARC grids into an abstract, object centric representation using a set of hand crafted heuristics.

Some of the work around these explicit abstract representations has been heuristic or hard coded, but sometimes compact representations of the grids into some other representation is actually an explicit part of the learning objective.

For some of the other approaches, while there may not be an explicit abstraction step, it's reasonable to assume that the layers of a neural net in say a fine-tuned LLM is actually learning such representations implicitly.

The idea of refinement comes up in a few of the papers. If we think of ARC in general as a grid > grid transformation problem, then one obvious thing we can do to break this down a bit is to try to construct the set of repeated transformations through partial grids:

                                                                  
       ┌─────────┐                                                
       │  Input  │                                                
       └────┬────┘                                                
            ├──────────────────────┬──────────────────────┐       
            │                      │                      │       
            ▼                      ▼                      ▼       
         ┌─────┐                ┌─────┐                ┌─────┐    
         │     │   ┌─────────┐  │     │   ┌─────────┐  │     │    
 null ──►│ f() ├──►│ Partial ├─►│ f() ├──►│ Partial ├─►│ f() ├──► 
         │     │   │ output  │  │     │   │ output  │  │     │    
         └─────┘   └─────────┘  └─────┘   └─────────┘  └─────┘

This can come in a few different forms for different approaches. For example with a LLM/VLM, we might repeatedly apply the LLM, providing partial grids as additional context after step 0, maybe even explicitly asking the LLM to correct any mistakes.

In some approaches there is a notion of grid similarity, and this can be a useful signal for training.

Ultimately allowing repeated applications of some function over grids can enable types of computation that might not be possible in say a single pass through a transformer, or any fixed compute function. Many ARC problems become much easier if you repeatedly apply some function, and this is usually helpful when there is some linear dependence between computational steps.

For an example of a problem that illustrates the importance of such iterative computation:

▼▼▼▼▼

This transformation function is much easier to write as a loop!

Thinking models, O3, inference time compute #

This wasn't covered in the technical report as it happened after in December, when OpenAI launched O3 with the announcement that it achieved an 87.5% score on ARC-AGI-1, on the semi-private eval set.

Just in June, the narrative was still that solving ARC-AGI would be extremely hard. This has totally flipped on its head in just a few months. Even those bullish about rumors of Q* and other reasoning approaches would not have expected this level of success.

This was an exceptional result, and even those labelled DL skeptics took a moment to acknowledge its importance. We have to take this seriously, and since O3, as well as DeepSeek, many people will be looking to leverage thinking models to approach ARC 2025.

Emulating and dramatically optimizing whatever OpenAI cracked for O3 would be a completely valid, and viable approach for anyone pursuing ARC in 2025, and it seems that several groups are already planning to do this, as Mike Knoop mentions at the end of his R1 analysis.

Letting LLMs think before answering is obviously a powerful approach:

It enables dynamic inference time computation. As mentioned above regarding refinement, this can be very useful for some puzzles.
There is still some discussion about what is under the hood, but there is some form of inference time scaling supported from thinking models, where multiple reasoning traces can be followed in parallel.
Thinking models are more akin to running programs, reasoning programs nonetheless. The ARC team refer to this as reasoning synthesis.
They can attempt to verify their answers, backtrack when they go wrong, and follow logical steps. This is very useful for a domain such as ARC.

At a high level, thinking tokens can form some kind of not entirely discrete program code and this is in my opinion a big part of what makes them so powerful. I've written a little more about this idea here.

Due to the fact that ARC is a verifiable domain it should be possible to use RL to train a thinking model specifically to solve ARC puzzles. If done right this can cause models to learn how to think about ARC tasks in a programmatic way, rather than just memorizing all of the patterns of the test set. The hope is this will greatly improve generalization ability. It might even be the case that the in-context learning of these models is a sufficient form of test time adaptation.

Training these models is fiddly, and probably expensive. I've done a little bit of exploration into this here (although this work is already likely well out of date), and there are now a lot of people in the open-source community building tools and doing research on replicating DeepSeek's RL result, with some successes on simpler domains than ARC even with small models.

The immediate challenge for these approaches is context lengths. Puzzle context itself can be 6K tokens or more, and for a decently sized thinking trace, you may want another 10-30K tokens or more! This is hard to fit on limited compute resources, but people are working on optimizing this.

Whilst O3 performed well on ARC-AGI-1, the new version of the competition slashes O3-low performance from 76% to ~4% (although it still holds the top spot on the unrestricted-compute leaderboard).

I expect to see an ARC optimized thinking model be one of the top scoring approaches for this year's competition, but it will require significant $$$ and some serious LLM expertise.

Core Knowledge Priors #

To solve ARC it is useful to have some basic knowledge and understanding of the world, as often puzzles leverage concepts that we are highly familiar with as humans.

A simple example is the notion of gravity. We all know what gravity is, and the concept even shows up in some ARC tasks:

▼▼▼▼▼

This knowledge dependency is impossible to avoid, but to minimize the impact this crystallized knowledge has on one's ability to solve ARC tasks, ARC restricts itself to building on a minimal set of knowledge called core knowledge priors, defined as:

cognitive building blocks that are either present at birth or acquired very early in human development with minimal explicit instruction, as described by the Core Knowledge theory.

It is very hard to come up with a complete list of core knowledge priors. They are discussed in On The Measure of Intelligence, and I'll pull out the summary of them from there:

Objectness and elementary physics: humans assume that their environment should
be parsed into “objects” characterized by principles of:

cohesion (objects move as continuous, connected, bounded wholes)
persistence (objects do not suddenly cease to exist and do not suddenly materialize)
contact (objects do not act at a distance and cannot interpenetrate)

Agentness and goal-directedness: humans assume that, while some objects in their environment are inanimate, some other objects are “agents”, possessing intentions of their own, acting so as to achieve goals (e.g. if we witness an object A following another moving object B, we may infer that A is pursuing B and that B is fleeing A), and showing efficiency in their goal-directed actions. We expect that these agents may act contingently and reciprocally.

Natural numbers and elementary arithmetic: humans possess innate, abstract number
representations for small numbers, which can be applied to entities observed through
any sensory modality. These number representations may be added or subtracted, and
may be compared to each other, or sorted.

Elementary geometry and topology: this core knowledge system captures notions of:

distance
orientation
in/out relationships for objects in our environment and for ourselves

After tagging 200 of the ARC-AGI-1 training dataset tasks, I also ended up producing my own taxonomy of something kind of like priors (perhaps more like concepts) across the different tasks, you can see that breakdown here. Other taxonomies of ARC problems include Concept-ARC.

ARC-AGI-2 #

The new version of the benchmark is a substantial step up in difficulty. The ARC team covers details of the changes in their blog post in depth, but I will summarize the delta here. To some extent, the benchmark was updated to really go after the deficiencies in the top scorers from last year's competition. This may seem unfair, but once again it is kind of the point - we can't really say we have full-blown AGI until we, as humans, are no longer capable of coming up with problems that we can solve that AI systems can't. Moving the goalposts is somewhat intentional!

There are a few specific types of problems that the team have explicitly incorporated into the new dataset that today's systems struggle with, which you can see examples of in the above blogpost:

Symbolic interpretation - "tasks requiring symbols to be interpreted as having meaning beyond their visual patterns"
Compositional reasoning - "tasks requiring simultaneous application of rules, or application of multiple rules that interact with each other"
Contextual rule application - "tasks where rules must be applied differently based on context".

In addition to the introduction of new tasks capturing the above, a bunch of tasks that were susceptible to brute force search have been removed from the private test set. This appears to be all tasks that were solved by Icecuber.

The datasets have changed slightly. In all the eval datasets there are now 120 problems, and the training set has expanded to 1000 problems.

The three eval sets, public, semi-private, private have been calibrated for human difficulty [6].

The hardware has been improved too, with significantly more GPU memory available.

The scores for 2024s top solutions have absolutely plummeted. Most LLMs out of the box now get 0%, ARChitects 1st place score of 53.5% is now down to 3%, and O3 is down from 76% to ~4%.

In summary, it's a much much harder problem set. Whilst human pass rates are roughly the same, my anecdotal observation is that these puzzles are still harder for humans, they require significantly more thought and take more time to solve[7].

The ARC ecosystem #

Outside of the direct research on approaches, there are a few useful resources for anyone starting to dig in. The arcprize.org site has a lot of useful information, guidance, and links to get started, as well as access to the Discord chat.

Simon Strandgaard's Awesome ARC page has a ton of links and resources, editors, tools, paper links, sample notebooks, prompts, etc etc.

Guillermo Barbadillo's literature review for his own 2nd place solution is a good read on some of the history, and was useful in preparing this content.

There is a lot of prior work in creating expanded training datasets (beyond the 400 and now 1000 for ARC-AGI-1/2) which are leveraged by a lot of the work discussed below, notably:

Re-ARC contains generators for all 400 of the ARC-AGI-1 training problems, so that you can generate more examples of these problems. Same problems, more samples.
Concept-ARC - groups ARC problems into concept groups, they then produce 10 new problems for each of the 16 concept groups, resulting in 160 new tasks.
ARC-Heavy (BARC) - provides 200k new problems, using LLMs for generation. This is a big dataset, it's not super clean, but it's a huge expansion of data for training.

And more, including some simplified problem sets, such as Mini-ARC, 1D-ARC, Sort-of-ARC, Language-annotated ARC (LARC).

A conceptual framework for ARC approaches #

To some extent, pretty much all the top ARC approaches actually follow a subset of a single high level recipe. The implementation details, representations, methods vary massively, but there is a general formula here that covers everything from discrete program search to LLMs with test time training:

Initial program guess: Guess 1 or more programs
Program search and improvement: Generate new programs, randomly, using a gradient, or hill climbing with some metric
Program selection: Select the best program(s), with many possible approaches to "best"
Program execution: Run your program(s) against the test input
Answer selection: Select your best answers if there are more than one

This does not describe pre-training for any of these approaches which vary significantly (or in some cases, there is none).

I'll cover the main two different approaches below within the context of this recipe:

The anatomy of a test-time-training approach (LLMs)
The anatomy of a program synthesis approach

Some more novel approaches fit here too, e.g Searching latent program spaces is the same pattern again, where a program is guessed (or a vector representation of a program), iterated on through gradient ascent, but then skips the selection step as there is only one, and has a novel approach to program representation and execution.

The anatomy of a test-time-training approach (LLMs) #

The top 3 scores this year did this - ARChitects, Omni-ARC, and MindsAI (unsubmitted/unpublished).

In the case of LLM fine tuning, the LLM is a program, and we can interpret the TTT approach for LLMs in the context of the general recipe as:

Our pre-trained model provides us a starting program guess, so no action required (at inference time)
Fine-tune / improve the program using gradients from the examples for each problem
We probably only have 1 program after fine-tuning, but could have multiple
Perform some kind of sampling of our program over the test input, often across augmented problem grids
Select the best answers from that sampling, using some metrics (like consistency across augmentations)

MLST has done a fantastic job of interviewing various people from these groups, and I've linked some of those podcasts next to the relevant papers below [8].

      ┌──────────┐                               
      │Base model│                               
      └─────┬────┘                               
            │  <augment>   ┌───────────────────┐ 
 <fine-tune>│◄─────────────│Public ARC problems│ 
            │              └───────────────────┘ 
      ┌─────▼───────────┐                        
      │Preliminary model│                        
      └─────┬───────────┘                        
            │  <augment>   ┌────────────────────┐
 <fine-tune>│◄─────────────│Private ARC problems│
            │              └────────────────────┘
      ┌─────▼─────┐                              
      │Final model│                              
      └─────┬─────┘                              
            │                                    
            │   ┌─────────┐                      
<augment_0> ├──►│Candidate├─────┐                
            │   ├─────────┤     │                
<augment_1> ├──►│Candidate├─────┤                
            │   ├─────────┤     │                
<augment_2> └──►│Candidate├─────┤                
                └─────────┘     │                
                                │ <unaugment>    
                  ┌─────────────┘                
                  │                              
              ┌───▼───┐                          
              │Scoring│                          
              └───────┘

Diagram is derived from the ARChitects paper, and captures the critical steps, pre-training, data augmentations, extended datasets, private set fine-tuning, candidate generation and scoring.

Most of these steps are fairly obvious. You get a base model, you fine-tune it, you fine-tune it some more on the private set, you use augmentations to enlarge your training datasets. The candidate generation and scoring is less obvious, and is discussed below.

Pretraining is a relatively straightforward part of the process:

Take a pre-trained LLM that is already filled with conceptual priors, and there are a variety of base models used in the papers that follow
Fine tuning LLMs across lots and lots of ARC problems, leveraging some of the synthetic datasets above so it gets better at the broad domain ARC grid problems
Perhaps fine tune on adjacent problems, as was the idea with Omni-ARC, in the hope of inducing better representations of the puzzles themselves

Transformer architecture optimizations #

Many people have had the intuition that ARC puzzles are spatial / vision problems, so what about VLMs? This is explored nicely in Mini-ARC and A 2D nGPT Model For ARC Prize, where small vision transformer models are trained from scratch, and a 2D positional embedding scheme is pulled together. There are of course many improvements here to try, but it doesn't seem any of the VLM based approaches have been engineered yet to a point of being competitive.

One challenge with LLMs is the number of tokens required. For larger puzzles, you have 30x30 grids. Given 3 example pairs and 1 test pair, that's 7x30x30 tokens minimum (6.3K). That's quite a lot of tokens, which, without a customized tokenizer, can easily double due to separators, newlines etc. You need to fit this all in memory too and it needs to run fast.

The ARChitects paper performs a few nice optimizations to make this all run fast. A custom tokenizer to prevent number chunking (12 is two tokens, 1,2 rather than just 12) for example, which seems to have a nice impact on efficiency.

TTT / TTFT #

Test-time training, or test time fine tuning is the most notable innovation for making LLMs competitive in ARC 2024.

The moment your submission starts up, it gets to see all (120) private eval puzzles. There are two things you can do here:

Continue your pre-training fine-tuning process on all private eval tasks to create one new and improvement model
Fine tune a new model for each of the tasks

Different groups went in different directions, although the 2nd place paper contrasts these approaches in a controlled way and finds that, probably as you would expect - fine-tuning per task yields better scores. However, it's more expensive to fine tune separately for each task, so there are trade-offs to make, and the best use of your limited compute is unclear. For example, ARChitects don't fine-tune per task whereas Omni-ARC does, but Omni-ARC uses a much smaller model.

Just to make it clear how one constructs the test time training set, you need to effectively create a new training set from the examples, as your code doesn't get to see the true answer for the test set actual problems! Omni-ARC's description of this is simple:

For each test problem that had n train samples, I fine-tuned the model using n-1 train samples and using the remaining sample as a test sample. The selection of the test sample was done randomly on the fly during training.

You effectively construct new in-context tasks out of the given sample pairs.

Data augmentations #

The second frequently used technique for fine-tuning dataset generation, both pre-training and test time, is to leverage augmentations of the data. You take a list of grid pairs, and apply a reversible transformation to each grid to create more problems. This is a common technique in ML and seems to be important to performance here too.

Some of the augmentations applied across different groups as an example:

Rotations, reflections, transpositions (this seems really important for LLMs, due to how much simpler it is for LLMs to "see” horizontal lines rather than vertical ones)
Color permutations
Reordering pairs
Padding
Upscaling
Problem augmentation (transformation on output only that more fundamentally changes the problem)

This is useful for training / fine-tuning, it will also come up in program selection and answer selection techniques!

Candidate generation and selection #

There are a few variations of this, but the high level idea is roughly the same. I'll summarize the ARChitects approach as well as the Omni-ARC approach, which we think is similar in principle to what MindsAI do too.

The primary objective here is to generate multiple answers, 10s to 100s, and then perform some selection process at the end. There are different ways to generate these variations, but both top prizes rely on augmentations to do this.

The ARChitects use quite a novel LLM token sampling approach, which is detailed a bit more in the paper notes. They sample tokens from the LLMs and explore multiple different token sequences, generating multiple answers whose overall token sequence is greater than some fixed probability. They use augmentations to then compute probabilities of solutions across multiple variations, and this feeds into the selection process, following the intuition that:

a correct solution should demonstrate greater stability in its sampling probability under augmented conditions compared to an incorrect one

For Omni-ARC, this process is much simpler. They set the temperature to 0, and run inference over 96 augmented versions of the puzzle. They reverse the augmentations, and then perform a voting mechanism across all the solutions to choose the best ones.

Ultimately the point is that we don't just ask the LLM to print its 1 best answer, we ask it to generate several answers, and then select the best ones according to some metric.

The anatomy of a program synthesis approach #

At this point with a background on DSLs, representations, and search, hopefully the basic brute-force approach is relatively clear at a high level, but framing the approach in terms of the general recipe:

Guess lots of programs, possibly from scratch or from a built up vocabulary
Continue to guess more programs, using some metrics for searching (like pixel error), or using NNs to guide that search (DreamCoder)
Select one or more correct programs, using some metric (like preferring short programs)
Execute our best program(s), possibly across augmentations
Apply some scoring or voting to select the best answers

The first obvious area for innovating is improving upon the representations for problems and the DSLs used. Sometimes it's pure Python, most often the representations are just grids. A lot of effort has gone into some approaches to hand design DSLs, some of which are quite innovative, for example with graphs and graph transformations, or by representing programs in some latent vector space.

Searching over programs could be straight up brute force, but usually include some hand-crafted heuristics for searching over programs. Most solutions follow a "shortest program" selection principle, so proceed with a roughly breadth first search, or beam search. DreamCoder provides a much more intelligent approach to program search, with NNs that can guide the search process and build up a vocabulary of useful building blocks.

Metrics are often defined to guide program search too, e.g in gradient-free search methods which may use evolutionary strategies or simple hill climbing, some measure of distance to the target grid can be used such as pixel error.

Program selection can have a few tricks, similar to LLMs, augmented versions of the problems are often used as part of the generation and selection process for programs and/or solutions. Shorter programs are nearly always preferred, or as with LLMs, consistency across augmentations.

Compute efficiency is absolutely crucial. Good program synthesis approaches need to be implemented in a fast language like C++. No one, yet, has found a way to use GPUs to help perform program search (perhaps with the exception of searching latent program spaces), but there are some discussions in the community I mention below around how this might be possible.

ARC 2024 papers review #

Relatively rough notes follow on all of the top paper prizes and runner ups. I didn't go into every winning solution, although the top 2 published scores both happen to have also won a paper award, so they are covered.

Top 5 private scores:

The ARChitects (53.5%) - Covered below.
Guillermo Barbadillo / Omni-ARC (40%) - Covered below.
Alijs (40%) - A guided brute force program search, well engineered specifically to ARC with human experience of the puzzles. Notebook link.
William Wu (37%) - An ensemble of previous prize winners. Notebook link.
PoohAI (37%) - More ensembling of previous years approaches. Notebook link.

Top 3 papers from ARC 2024:

Combining Induction and Transduction for Abstract Reasoning
The Surprising Effectiveness of Test-Time Training for Abstract Reasoning
Searching Latent Program Spaces

Runners up:

The LLM ARChitect: Solving ARC-AGI Is A Matter of Perspective
Omni-ARC
Mini-ARC: Solving Abstraction and Reasoning Puzzles with Small Transformer Models
Towards Efficient Neurally-Guided Program Induction for ARC-AGI
A 2D nGPT Model For ARC Prize

Combining Induction and Transduction for Abstract Reasoning #

Paper: Combining Induction and Transduction for Abstract Reasoning

Shows that a combination of transductive and inductive methods are effective and solve relatively different tasks and can be ensembled together well, create a new dataset, and perform a bunch of experiments, ablations, etc.

This is the paper that introduces the ARC-Heavy (BARC) dataset, which is a massive dataset of extended ARC puzzles generated by LLMs. This is a very useful contribution to the ecosystem that many others have leveraged for their own solutions.

Induction Intuitively, induction captures the notion that a learner should first explain the training data, then use that explanation to make predictions.

Transduction Transduction instead captures the intuition that the training examples themselves should play a direct role in generating new predictions, and that successful prediction need not require an explicit explanation

That induction and transduction are complementary is the main claim of the paper. Over 400 problems, 26 solved only by induction, 19 solved by transduction and induction, 35 solved by only transduction.

What overlap would you expect if these were completely uncorrelated? Approximating both as a ~12% solve rate which they roughly are (45/400, 54/400), the overlap would be expected to be 0.12^2*400 = 6 (as opposed to 19).

They are somewhat independent, not completely independent, and definitely not anti-correlated. Independence is definitely useful in an ensemble though.

Generated 400K synthetic arc problems, and noted that the more synthetic problems generated, the better the overall performance.

They also note that the amount of test time compute has a logarithmic impact on the result.

Overall, they get a pretty good score on the public eval (36.5%). The method is too expensive though, and performs poorly when scaled down enough to fit in the kaggle environment, where it only scores 19%. Synthetic data is super powerful then it seems!

If you could customize this architecture to ARC with a bespoke NN that was much smaller, perhaps it could pay off. The authors note:

this suggests a strong payoff for smarter neural program search

Authors also highlight a problem I experienced myself. The RE-ARC verifier programs are so crazy that it is hard to use them as any sort of training data:

ReARC is implemented in a domainspecific language, and lacks natural language annotations, making it difficult to remix with LLMs

What is the line between transduction and induction? Perhaps the optimal solution here is somewhere between the two, authors suggest such an idea:

One way of implementing this idea is to do program synthesis within a language whose atomic primitives are non-symbolic, and to pretrain those primitives to encapsulate the basic atoms of core knowledge. While work has taken steps in related directions ... how to engineer and scale this idea remains open

Some sort of soft programs (non-symbolic), not dissimilar to what probably happens in reasoning / thinking LLMs, but could be more focused toward ARC.

The Surprising Effectiveness of Test-Time Training for Abstract Reasoning #

Paper: The Surprising Effectiveness of Test-Time Training for Few-Shot Learning

TL;DR - Test time fine-tuning is effective, and boosts ARC pass rates in their setup from 17.5% to 45% when compared to just fine-tuning at training time.

The paper provides a good taxonomy of various design choses for TTT, different types of loss, shared or task specific fine tuning, data generation approaches, augmentations for training and different approaches for voting / candidate selection, etc.

They perform a bunch of ablations, that generally seem to indicate that many of the methods in this paper offer some improvement in performance for ARC:

Leave-one-out tasks, one of the 3 ish provided input/output pairs is held back and predicted, and the remaining task pairs are provided as context (as opposed to just directly training against each input/output pair without any context from other tasks)
Using a demonstration loss, such that the model is also tuned to predict its demonstration examples, as well as the held out test example
Performing per task TTT rather than just shared TTT across all hidden tasks
Transformations of the grids, vertical and horizontal flips for example, performing training and predictions across augmented views of the data

There is also some good data on voting approaches across transformations, which are compared to an Oracle (that selects the best answer if present). The number of examples here is relatively low though, and no confidence bounds are given, so it's hard to make strong conclusions that differentiate between simple voting and hierarchical voting, but it seems clear that multiple augmentations are better than 1.

If you want to understand how various design choices for LLM TTT on ARC affect performance, this is a great place to start.

Searching latent Program Spaces #

Paper: Searching Latent Program Spaces
Interview (MLST): Spotify

They introduce the latent program network, which learns a distribution over latent programs in a vector space, enabling a gradient based search for programs, as well as a "neural decoder" that can execute the programs on specific inputs.

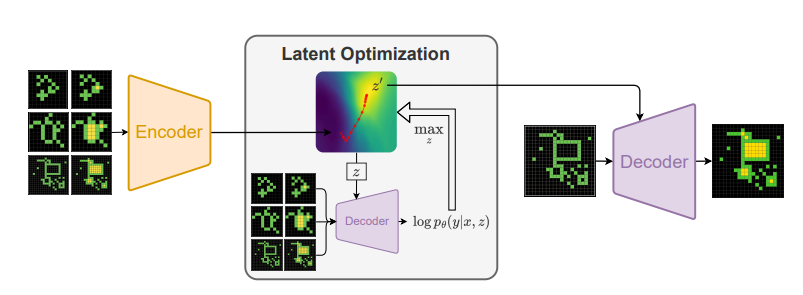
Scores 3% on test, 9.5% on eval, up to 46% on training (did not completely converge).

This is pretty hardcore, and conceptually very novel, all trained from scratch without pre-trained LLMs. At a high level they do the following:

They come up with a vector representation of "programs" (of dimension 256) for ARC
They take a task sample(s), and encode it into the latent program space, i.e - predict the program's vector representation based on input and output
They then perform gradient "ascent" through the latent program space to try find a better program than the initial guess of the encoder (and can do this, because it's differentiable)
They take the best program they have found (or its latent vector representation) and run it through a decoder that turns it back into a pixel grid for the test problem
"The probabilistic decoder is responsible for mapping a latent program and an input to the space of outputs, directly predicting the output pixel by pixel instead of via a DSL"

Training is pretty complicated, and the paper provides a lot of the details and some clever tricks if you want them (this was also close to my skill limit), but some highlights:

Seems like it's trained e2e, it's a full differentiable network after all
Importantly, to avoid collapse, for each problem which has N sample input output pairs, they use N-1 tasks to predict one of the other tasks
Both the encoder and the decoder are small transformers that take in flattened padded grids as inputs

This is ultimately a program search. By embedding programs in this vector space with an encoder, the entire thing becomes differentiable, which allows an efficient search process to happen within the space of programs using gradient descent, and this appears to be absolutely critical to the performance of the approach. One-shotting the program in the encoder performs significantly worse.

Decoder backward pass is quite expensive, which makes the latent optimization (gradient ascent step) slow.

5 TPU days to train, not cheap but not expensive. Did not converge. Does not appear to use any of the extended task sets, and it appears they did not use the evaluation data set for the training a model against the final test set. Looks like there is headroom here.

The LLM ARChitect #

Paper: The LLM ARChitect: Solving ARC-AGI Is A Matter of Perspective
Interview (MLST): Spotify

A great reference for test-time fine tuning!

Fine tuning an LLM, with an expanded dataset, test-time fine tuning with data augmentations, multiple candidate generation, scoring. Fine tuning for the entire test set, not per task.

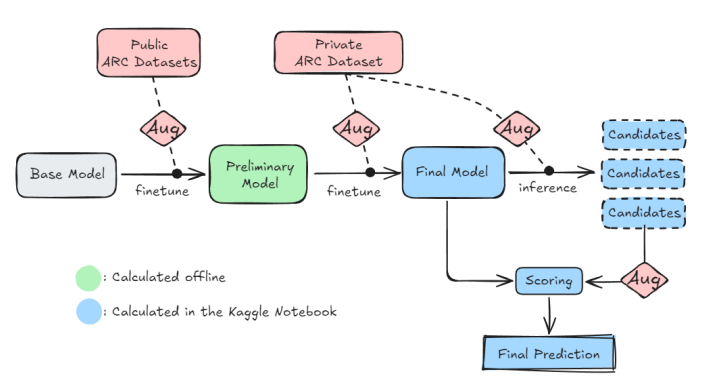
The expanded dataset was big! Using all the additional datasets available, and a lot of augmentations. This led to over 500k training examples for their largest model (considering the base training + eval sets are 700/800 tasks).

Updates to the tokenizer to just represent 64 symbols. Tokenization is a problem, due to e.g number grouping which would probably be catastrophic (12 being treated as "12", not "1","2"). Often we just put commas, or spaces between the numbers, but this doubles the token count.

Augmentations - rotations, transpositions, permutations of the colors, example order.

Using small base models, e.g Llama-3.2-3B-instruct, Mistral-NeMo-Minitron-8B-Base.

Initially trained on Re-ARC + 75% of the public evaluation set using LoRA.

Trained further on the hidden dataset during inference (test-time training), spending around 5 hours on the Kaggle GPUs.

Provides a detailed take on candidate generation. Each token in an LLM is generated with some probability. The greedy sampling approach is to take the token with the highest probability, but this will produce just one sample. Alternatively you can sample tokens stochastically, say proportional to their softmax probabilities, and generate several candidate solutions this way.

Here they do something custom - they sample tokens stochastically, but keep track of the overall sequence probability (assumed to be the product of token probabilities), and if this overall probability drops below some threshold then the sequence is discarded. It's faster as you can leverage caches, more memory efficient, and it boosts performance over simple greedy/stochastic approaches, and generates many candidates.

Candidate selection leverages the augmentations. By augmenting the solution candidates, for each augmentation, you can ask again what the probability of the model generating that sequence of tokens would be.

Given a set of probabilities of the solution under different augmentations, the authors take the as the selection metric (or ). The intuition here is effectively that:

a correct solution should demonstrate greater stability in its sampling probability under augmented conditions compared to an incorrect one

So they chose a solution that performs well across many augmentations.

They were given some compute from Lambda Labs, using 8xH100s, they ran a lot of experiments and variations over time. You definitely need some $$$ for this kind of approach and experimentation, I'd guess they spent on the order of $30K compute, could be more if they had it for longer.

Omni-ARC #

Paper: Solution Summary - arc24

Not wildly dissimilar to ARChitects. LLM based approach, some novel angles in here:

Fine tuning on ARC-related tasks, not just the tasks themselves
Similar augmentation, test time fine tuning as ARChitects
Some exploration and future research in building models for verifying correctness (and better answer selection)

The insight presented at the beginning is that to learn a good representation, we should train on multiple adjacent tasks from the tasks themselves. The author lists these:

The original ARC task itself (predict the unknown output, transductive)
Generating new inputs from other inputs
Generating code to solve the tasks (inductive inference)
Executing code on a grid to produce an output
Generating new grids from grid generating code

Hence "Omni”. More auxiliary tasks, better representations, is the idea, although in the end this idea was only partially executed on it seems.

The model used Qwen2.5-0.5B-Instruct as a base model, fine-tuned using LoRA on augmented datasets and some auxiliary problems as discussed. Test time fine tuning is integrated, and notably produces a fine-tuned model for each task as opposed to all.

Inspired by the MindsAI approach, and references some of their work, AIRV (which I can't find details on) which stands for Augment, Inference, Reverse Augmentation and Vote, and this is used for candidate generation and selection. It's not explicitly written down or I am missing it but I will assume this means roughly:

Problems are augmented to create several variant problems
Augmentations are what drive 96 solution proposals, as temperature is set to 0
Solutions to augmented problems are inverted back to their original form
A simple voting mechanism is used to choose the best answers

At the end, it's ensembled with the 2020 solution (looks like Icecuber). Without the ensemble, the score is 32% (I think, the graph does not match the text).

A few follow ups and thoughts for the future from the author:

Rather than using voting for generation selection, they trained a model to predict correctness. Didn't seem to impact performance on the test set, but showed promise on evaluation.
Notably, they tried to add BARC/ARC-Heavy dataset to the training data, but didn't see much improvement from it, which was surprising.
Did try larger models, but fine-tuning was slower, context was a challenge (which ARChitects addressed somewhat with their custom tokenizer).
Is interested to see how thinking / reasoning models can perform.

Author notes:

The approach of using a transformer and test-time fine-tuning could likely keep improving and maybe solve the ARC prize if we generate enough synthetic data to densely cover the space of the ARC problems. However that kind of solution won't give us more knowledge about how to reach AGI

Mini-ARC: Solving Abstraction and Reasoning Puzzles with Small Transformer Models #

Paper: Mini-ARC: Solving Abstraction and Reasoning Puzzles with Small Transformer Models

A good place to start if you are interested in vision transformer approaches!

Uses small vision transformers trained from scratch, with TTT. uses some novel positional encodings and color embeddings, and also explores an approach using refinement that yields some improvements.

Used a lot of the augmented datasets, RE-ARC and BARC/ARC-Heavy, as well as the authors own extended dataset ARC-HTML.

Doesn't submit an actual score to the competition, as the architecture is limited to 12x12 grids, but reports 41% on a subset of the public eval set.

Refinement - the general idea here is to allow the model to take multiple passes, initially making a guess at the output, and then feeding both the partial output and the context back in and refining it. It seems to provide a small but probably significant boost to performance, and is not seen in many of the approaches.

The paper exposes one general issue with context lengths. For larger puzzles, you have 30x30 grids. Given 3 example pairs and 1 test pair, that's 7x30x30 tokens minimum (6.3K). That's quite a lot of tokens, which, without a customized tokenizer can easily double due to separators, newlines etc. You need to fit this all in memory too.

Towards Efficient Neurally-Guided Program Induction for ARC-AGI #

Paper: Towards Efficient Neurally-Guided Program Induction for ARC-AGI

The authors start with the general statement of DLs deficiencies when it comes to open domains, and generalizing outside of the training set distribution - which is particularly relevant for ARC.

In the context of ARC they say that "This encourages research on extending the out-of-distribution generalization capabilities of learning systems". This is a super important aspect of ARC in general and is key to succeeding in the benchmark.

They cover a couple of different approaches and experiments, and one that is not explored but proposed:

Approach 1: Learning the grid space

Objective here is to learn some concept of distances between different grids
This is done by performing random (1-8) transformations on randomly sampled grid patches in order to train a model to estimate distance
This can then be used as a heuristic that feeds into a discrete program search process

Approach 2: Learning the program space

A vision-language transformer architecture generates program tokens for some DSL from some input output grid pair
This is turned into a probability distribution, somehow, and programs are then enumerated from that distribution (with probability greater than some threshold)
Their generated DSL is a custom and they generate a syntax tree of it
It looks like the training for this is very hard coded, programs are generated, using sampled ARC grid patches again, or randomly, but the authors are explicitly pulling out "patterns" observed in the problems

Approach 3: Learning the transform space

This is an extension to learning the program space, but with a refinement component to it - so that intermediate grids can be produced, and programs refined from each step.
This is explored but authors note they ran out of time to go deeper here.

The program search component is absolutely crucial to performance.

Actual results are low, 5.8% on public eval overall, but this was more of an exploratory paper, and on their subset of solvable tasks they get up to 80% ish.

This is a good quote from the authors that I've been thinking about a lot recently:

ARC-AGI is fundamentally not a grid-to-grid problem ... most of the steps involved in solving an ARC-AGI task are not strictly grid-to-grid transformations and thus do not result in an intermediate grid that can be evaluated for its similarity to the target ... instead can be thought of as a sequence of intermediate program states which themselves are lists of various kinds of intermediate objects and values. As such, the grid-to-grid similarity concept only potentially allows guiding a small portion of the overall search for a solution.

Quite a lot of effort went into the DSL. It is surprising to me just how many of the approaches seem to hand-code a DSL, rather than trying to learn one, or use an existing one.

Authors feel that their main limitation here is the DSL, noting that it's too high level and specific.

A 2D nGPT Model For ARC Prize #

Paper: A 2D nGPT Model For ARC Prize

A small (42M param) 2D transformer, test time training. Built on top of normalized transformers (nGPT).

A grid cell attends to all cells in the same row and same column. They use rotary position embeddings (RoPE) here. They also experimented with adding a single attention across the whole grid, but this didn't pan out.

Restrict themselves to constant size tasks, of which there were only 262/400. They extended the dataset using RE-ARC, they also increased the training set using invertible transformations.

One issue highlighted during TTT is that of task blurring:

For instance, in the task of figure 2 above, holes are filled with yellow. If we apply color permutations, then we could get pairs where holes are colored with, say, cyan. This prevents the model from learning which color has to be used for filling holes

This seems like it would be an issue for many augmentation approaches, although this is the first place I've seen it mentioned so far. No solution is offered, the additional augmentations outweigh the blurring issue.

No official score provided, 26% on the constant sized evaluation tasks, most likely < 15% on the hidden test set if they had managed to run it. Could be a useful reference for any 2D / vision approaches, and similar overall in spirit to Mini-ARC.

Other notable papers / ideas / approaches #

Getting 50% (SoTA) on ARC-AGI with GPT-4o #

Write-up: Getting 50% (SoTA) on ARC-AGI with GPT-4o

The idea here is quite simple - get GPT-4o to generate thousands of Python programs that attempt to implement a transformation for each puzzle, with some selection process.

Thousands (~8K) python programs are generated for each problem
Multimodal representations are passed into the model, both image and text representations
Lots of prompting to encourage reasoning (this was pre-O1)
A revision / refinement process, whereby the top N answers (based on a pixel error hamming distance like metric) are then iteratively improved on, feeding diffs back into the LLMs to correct efforts ("I was surprised by how much revision helps.")
A final voting selection process

The results on the public eval set were impressive and the best at the time, getting 50% which, if you ignore the program compute limits, was effectively SOTA[9].

Again, noting that this was pre-O1, it was a very clear example of the logarithmic returns one can get from the inference time scaling paradigm.

It's also different from other program search approaches in that it's using a complete and general language - Python. This makes a lot of sense when using a pre-trained language model, which has already been trained on an incomprehensible amount of Python code.

Author gives a pretty contra-Chollet take:

I think ARC-AGI will be one benchmark among many that just gets solved by scale

I'm not sure where people stand on this now, though, as attention shifted towards O1 like approaches. The costs spent on this at the time were high (someone privately shared with me they estimated around $10K to run this against the 400 public eval tasks).

It's also a nice example of program induction, and leveraging LLMs for that. Despite its conceptual simplicity or lack of fine-tuning (although there are tons of tricks in the execution of this to get it to work well), the results are very good and this is an important point in the history of ARC.

Icecuber (ARC 2020 winner) #

Paper: ARC-solution/ARC-solution_documentation.pdf

The OG discrete program search approach for ARC.

Somehow this work seems to be both completely aligned with, and completely antithetical to - the bitter lesson. Just search, but with a very well constructed (by a human) DSL.

There's not a huge amount to explain here and the paper/docs are very short. They wrote efficient C++ code for 142 unary functions (notably derived from 42 n-ary functions). They then search the space of up to depth 4 programs, searching depth 3 programs, depth 3 programs with diagonal flip augmentations, and then depth 4 programs until they run out of time.

Solutions are selected based on accuracy for the samples, and then following again the principle that shorter solutions (lowest depth) are better. A few tricks in here that are seen elsewhere too:

Augmentations (diagonal flips)
Color remapping according to some heuristics

There is some procedure at the end that I don't quite follow around combining "pieces", stacking image lists, moving things to origin, resizing for output grids.

This solution highlights a few things for me:

Efficiency of implementation is very important
A good DSL is actually very important
Augmentations are important

The first of these is sometimes overlooked by others, and we'll see elsewhere program search approaches in Python. DSLs are important and this is probably an uncontentious claim, but the best way to win with DSLs is to get a human to make one. Augmentations come up over and over again in nearly all solutions, both LLMs and discrete program search, and it's nice that this came up all the way back in 2020.

DreamCoder #

Paper: DreamCoder: Growing generalizable, interpretable knowledge with wake-sleep Bayesian program learning

Explanatory video: https://www.youtube.com/watch?v=qtu0aSTDE2I

Covering this as background for DreamCoder based ARC approaches.

DreamCoder performs inductive programming. Given a list of examples, it will attempt to generate a program that produces the demonstrated behavior (so, a perfect fit for ARC!). This is not ARC specific, it's a general approach for program synthesis.

One of the key aspects of DreamCoder is its wake-sleep algorithm. DreamCoder builds up a library of concepts, smaller programs that do specific things.

With a library of programs, during the wake phase you can search for discrete programs that solve your problem. This is a search problem, you can combine, compose functions from the library, or construct entirely new functions, to create a large search tree of programs that may or may not solve the task.

DreamCoder uses a learned model (the recognition model, like a policy network) to guide this search process.

Shorter programs are considered to be better, a result of Solomonoff's theory of inductive inference.

During the sleep/abstraction phase, the library of concepts is grown, with the intention of compressing programs. Commonly used sub-programs are pulled out as concepts, effectively programs are (re)factorized. The overall length of the library programs + the length of the solution programs is minimized.

During the sleep/dreaming phase, the goal is to train the model that drives the search process. You want to know what might be the best programs to explore for a given task.

There are two sources of training data here that are mixed together:

New programs p are drawn from the library randomly, executed given an input x to produce an output y.
Programs found for our actual tasks are also fed in, programs that solve specific problems, also giving us a p, and an x, y pair.

The goal of the recognition model is to predict useful programs p from a given input output pair x, y.

Wake, sleep (abstract, dreaming), repeat.

Neural networks for abstraction and reasoning: Towards broad generalization in machines #

Paper: Neural networks for abstraction and reasoning: Towards broad generalization in machines

This is a DreamCoder based approach, where the authors provide:

A language (DSL) called PeARL for working with ARC tasks
A new recognition model architecture

It's the best DreamCoder approach at the time of the paper, but its performance is still fairly modest, reporting 18/400 (4.5%) on the ARC-AGI-1 eval set, beaten by stock LLMs like GPT-4, and smashed by the winning 2020 brute-force DSL search (Icecuber) approach (fast search is still beating smart search, for now!).

The recognition model is customized, and they elect for an image based feature extractor using a small conv net like architecture, given the 2D, image like properties of ARC tasks.

They also have to deal with the fact that there are actually several images in an ARC task, inputs, and outputs. At a high level, they compute feature vectors from input and output grids, compute the difference, then average across samples to create a 256 dimension feature vector for an entire task.

They introduce another DSL called PeARL. They created a DSL for ARC, with relevant primitives such as grids and colors, and programs map from grid > grid. This doesn't appear to be the most complete DSL, I'm not sure why they didn't use e.g ARC-DSL.

The authors note that:

The design of primitives for PeARL has a big effect on the system's performance and is perhaps the most critical implementation detail.

As we've seen elsewhere, the DSL is extremely important.

In the end, they end up with a fairly substantial 77 primitives! This includes things like flips, rotations, transpositions, cropping, stacking, filling holes, counting colors and pixels, etc etc.

I suspect there is a lot of headroom here, improvements to the DSL, recognition model, etc etc. DreamCoder as a baseline architecture still feels like a good candidate for smart-search that actually works, but execution is everything.

CompressARC: ARC-AGI Without Pretraining #

Paper: ARC-AGI Without Pretraining | iliao2345

A recent, and conceptually interesting take on ARC. The paper is very theoretical at times and I was not able to follow it fully in depth, but it does influence some of my conceptual takes above.

By framing ARC as a compression problem, the authors show an approach toward benchmark that does no pretraining whatsoever, and get 20% on the public evaluation set.

So for each task:

Construct a specific neural network for that task with randomized parameters, which has a few equivariances built in, such as the permutations of the input/output pairs
The network produces 3x2 input/output pairs
It is optimized to reduce the reconstruction loss for 5 of the grids produced (the final grid being the answer that must be provided, so no known answer)

Intuitively, by attempting to encode all the grids into a neural network's parameters with the correct loss - this results in some form of compression. That compression is forced to capture relationships between input and output grids, which are then useful to actually solving the problems.

How do you optimize for compression? The authors lay out why and how with a few tricks, and this seems in the end to boil down to a KL divergence penalty on the network parameters against a fixed normal distribution.

Given the lack of pre-training, this is basically nearly entirely test time adaptation. Not 100%, because there is clearly a ton of priors and bias fed into the neural network architecture that is specifically related to ARC. It's clear from all the other solutions that test-time adaptation is necessary, but is it really sufficient?

The idea that compression is related to intelligence is not new, and has been championed by M. Hutter, with, for example, the Hutter Prize. Here's a passage from the authors, which notably calls out several other theories referenced in here that are relevant to other approaches:

This equivalence between intelligence and compression has a long history. For example, when talking about intelligent solutions to prediction problems, the ideal predictor implements Solomonoff Induction, a theoretically best possible but uncomputable prediction algorithm that works universally for all prediction tasks. This prediction algorithm is then equivalent to a best possible compression algorithm whose compressed code length is the Kolmogorov Complexity of the data. In our work, we try to approximate this best possible compression algorithm with a neural network. A related measure of complexity is known as the Minimum Description Length.

You could imagine a derivative benchmark to ARC-AGI, inspired by the above and the Hutter Prize, that would require people to construct an algorithm that optimally compresses all the grids across all 120 problems. I've not seen any such derivative benchmarks yet, but investigating optimal compression of the ARC problem grids does seem like it could yield valuable insights.

Note: I read this before covering the older paper Object-centric Models and the MDL Principle below which builds on similar ideas and goes after compressed grid representations to solve ARC.

Graphs, Constraints, and Search #

Paper: Graphs, Constraints, and Search for the Abstraction and Reasoning Corpus

ARC tasks are 2D arrays of pixels. But when a human looks at a task, they don't "see" pixels. For most tasks you almost immediately perceive the grids as a set of objects. Object-centricity is a critical part of how humans solve ARC problems.

So there is a core problem of representation here. What is the best representation for the grids? It looks like there are some very inexpensive improvements to the representation that we can get, e.g "Doubling o1-preview performance on ARC-AGI with one simple trick". Similar approaches explored by Agemo here, and most in depth by the paper covered next - Object-centric Models and the MDL Principle.

The authors here choose an object centric graph representation, and then effectively search through a DSL of programs that operate on these graphs.

The representations are generally smaller[10], and this helps in reducing the search space.

There is a notable observation that the procedure to generate the graph representation from the pixels is 1-many. There are multiple different "interpretations" of the grid (think e.g the classical duck/rabbit illusion):

defining multiple abstraction processes improves ARGA's ability to correctly capture object information from the input images

Here's roughly what they do then:

Turn the grids into one or more graph representations
Do a greedy search over a sequence of graph operations (program), leveraging pixel error as a metric to prioritize the best graph program

ARGA is currently implemented in Python while the Kaggle solution is implemented in C++

This is crazy! I get it, but the performance gains left on the table here are massive, depending on their exact implementation, possibly 10-100x or more if this isn't multi-threaded.

It doesn't look like they actually posted an official score, but when compared against Icecuber on an object-orientated subset of the (presumably) public evaluation problems, it scores 35.6% compared to 40%. How a solution like this would generalize to some of the other non-object centric problems is going to be a part of the challenge, but could be side-stepped with some ensembling in the short term.

Object-centric Models and the MDL Principle #

Paper: Tackling the Abstraction and Reasoning Corpus (ARC) with Object-centric Models and the MDL Principle

Based on previous work that shows that humans often solve ARC problems in an object-centric way.

Related to the ideas discussed around compression, the authors use the minimum-descriptor-length principle to parse the grids into an object centric representation, with the intuition that "the model that best describes the data is the model that compresses them the most".

Their object centric representation of grids ends up looking something like the following:

  Layers(Vec(12,13), black, [
    Layer(Vec(2,4), Colored(Rectangle(Vec(2, 2), Full), yellow),
    Layer(Vec(1,3), Colored(Rectangle(Vec(4,4), Full), red)
  ])

These models can be used in a few different ways, to predict output grids, to describe a pair of grids jointly, and also to even create a new pair of grids for a task.

By finding the most compressive representation of the grid pairs, they are effectively learning about the structure of the task itself - compression leads to understanding, and this is highly related to the work in CompressARC.

This is only a light summary, the paper is quite dense, I need to spend more time on it, and it doesn't lay out all of the details of how their system works, but conceptually this is a very interesting idea.

HVM and NeoGen: Program synthesis with GPUs #

One relevant discussion I will highlight to this work is that of ViktorTaelin, good summary on reddit here.

All the program synthesis approaches today work on CPUs. What if we could leverage GPUs for this process? It could offer a massive increase in performance, not necessarily a change in complexity, but in brute force speed for sure as we can simply access more FLOPS, and right now that is the winning approach (simple fast search) rather than intelligent / smart searching approaches within the program synthesis approaches.

I follow Viktor, and while he is obviously incredibly smart I struggle to keep up with what he is talking about most of the time. But, he talks about ARC, and seems to be investigating leveraging his company's HVM system - a general purpose functional program evaluator (based on something called interaction nets, the best explanation of which I have found is here) that can be automatically optimized for GPUs so you don't have to write CUDA kernels - to attempt program synthesis on ARC.

I'd love to see where this goes. Running, evaluating, searching through programs on GPUs could be a game changer, but I haven't seen anything concrete yet.

reply via email twitter

Notes

[0]: Efficiency here is in terms of compute, not time.
[1]: based on our possibly flawed observation of our own minds
[2]: Well, arguably there is an explanation in the weights, we just don't know how to interpret them well enough
[3]: It is literally a program
[4]: The exception here seems to be the The LLM ARChitect
[5]: Except that it's well known, and there is a lot of Python code we can train on, which can make it useful in some program synthesis approaches that leverage large pre-trained LLMs
[6]: This is a notable difference from ARC-AGI-1, where we saw private test scores well behind public eval scores
[7]: like a full 5 minutes thinking in cases, compared to before where most problems would be obvious within 10 seconds after some practice
[8]: Minds AI / Mohamed Osman episode is here as there is no paper section for this
[9]: And seems likely to have contributed to the ARC team introducing a public leaderboard alongside the private one
[10]: Well compressed?

< lewish

ARC-AGI 2025: A research review